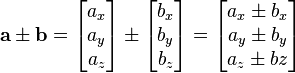Deducción del módulo de la suma

Escrito el 20 de Mayo de 2010 en español con un tamaño de 8,07 KB

Deducción del módulo de la suma

Este artículo presenta una deducción para la expresión del módulo resultante de dos vectores

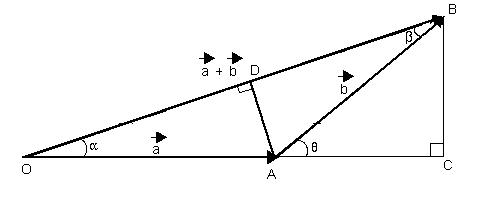
Sean dos vectores $\vec{a}$ y $\vec{b}$ que forman un ángulo ? entre sí:

La fórmula para calcular $\left| \vec{a} + \vec{b} \right|$ se deduce observando los triángulos rectángulos que se forman, OCB y ACB, y aplicando el Teorema de Pitágoras. En el triángulo OCB:

OB² = OC² + CB²

$OB = | \vec{a} + \vec{b} |$

$OC = \left| \vec{a} \left| + AC \right. \right.$

Resultando:

$\left| \vec{a} + \vec{b} \right|^2 = \left( | \vec{a} | + AC \right)^2 + CB^2$

En el triángulo ACB :

$\frac{AC}{| \vec{b} |} = \cos \theta$

$AC = | \vec{b} | \cos \theta$

$\frac{CB}{| \vec{b} |} = sen \theta$

$CB = | \vec{b} | sen \theta$

Sustituyendo esto en la igualdad de antes resulta:

$\left| \vec{a} + \vec{b} \right|^2 = \left( | \vec{a} | + | \vec{b} | \cos \theta \right)^2 + \left( \left| \vec{b} | sen \theta \right)^2 \right.$

$\left. \left| \vec{a} + \vec{b} \right|^2 = | \vec{a} |^2 + 2| \vec{a} | | \vec{b} \right| \cos \theta + \left| \vec{b} \right|^2 \cos^2 \theta + \left| \vec{b} \right|^2 sen^2 \theta$

$\left. \left| \vec{a} + \vec{b} \right|^2 = | \vec{a} |^2 + 2| \vec{a} | | \vec{b} \right| \cos \theta + \left| \vec{b} \right|^2 \left( \cos^2 \theta + sen^2 \theta \right)$

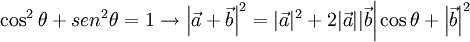
$\left. \cos^2 \theta + sen^2 \theta = 1 \rightarrow \left| \vec{a} + \vec{b} \right|^2 = | \vec{a} |^2 + 2| \vec{a} | | \vec{b} \right| \cos \theta + \left| \vec{b} \right|^2$

$\left| \vec{a} + \vec{b} \right| = \sqrt{\left. | \vec{a} |^2 + 2| \vec{a} | | \vec{b} \right| \cos \theta + \left| \vec{b} \right|^2}$

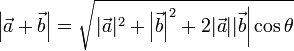
$\left| \vec{a} + \vec{b} \right| = \sqrt{\left. | \vec{a} |^2 + \left| \vec{b} \right|^2 + 2| \vec{a} | | \vec{b} \right| \cos \theta}$

Operaciones con vectores

Suma de vectores

Para sumar dos vectores libres (vector y vector) se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Método del paralelogramo.

Método del triángulo.

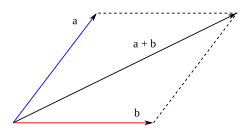
Método del paralelogramo

Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, completando un paralelogramo trazando rectas paralelas a cada uno de los vectores, en el extremo del otro (ver gráfico a la derecha). El resultado de la suma es la diagonal del paralelogramo que parte del origen común de ambos vectores.

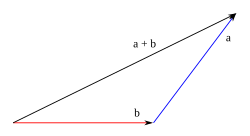
Método del triángulo

Consiste en disponer gráficamente un vector a continuación de otro; es decir, el origen de uno de los vectores se lleva sobre el extremo del otro. A continuación se une el origen del primer vector con el extremo del segundo.

Método analítico para la suma y diferencia de vectores

Dados dos vectores libres,

$\mathbf{a} = (a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k})$

$\mathbf{b} = (b_x \mathbf{i} + b_y \mathbf{j} + b_z \mathbf{k})$

El resultado de su suma o de su diferencia se expresa en la forma

$\mathbf{a} \pm \mathbf{b} = (a_x \mathbf{i} +a_y \mathbf{j} +a_z \mathbf{k}) \pm (b_x \mathbf{i} +b_y \mathbf{j} +b_z \mathbf{k})$

y ordenando las componentes,

$\mathbf{a} \pm \mathbf{b} = (a_x \pm b_x) \mathbf{i} + (a_y \pm b_y) \mathbf{j} + (a_z \pm b_z)\mathbf{k}$

Con la notación matricial sería

$\mathbf{a} \pm \mathbf{b} = \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} \pm \begin{bmatrix} b_x\\ b_y\\ b_z\\\end{bmatrix} = \begin{bmatrix} a_x\pm b_x\\ a_y\pm b_y\\ a_z\pm bz\\\end{bmatrix}$

Conocidos los módulos de dos vectores dados, $\mathbf{a}$ y $\mathbf{b}$ , así como el ángulo ? que forman entre sí, el módulo de $\mathbf{a} \pm \mathbf{b}$ es:

$|\mathbf{a} \pm \mathbf{b}| = \sqrt{a^2 + b^2 + 2ab \cos \theta}$

La deducción de esta expresión puede consultarse en deducción del módulo de la suma.

Deducción del módulo de la suma

Operaciones con vectores

Suma de vectores

Para sumar dos vectores libres (vector y vector) se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Método del paralelogramo

Método del triángulo

Método analítico para la suma y diferencia de vectores

Dados dos vectores libres,

Entradas relacionadas: