Péndulo Balístico: Principios, Cálculos y Aplicaciones
Clasificado en Informática
Escrito el en  español con un tamaño de 12,61 KB
español con un tamaño de 12,61 KB
El péndulo balístico es un dispositivo práctico en el cual ocurre un choque inelástico. Hasta la llegada de los instrumentos modernos, el péndulo balístico se usaba mucho para medir la rapidez de los proyectiles.
En este dispositivo, se le dispara un proyectil a un bloque pesado de madera suspendido. Inicialmente, el bloque de madera está en reposo. Después del choque, el proyectil queda incrustado en el bloque. Un poco de energía cinética se transforma en calor y en sonido, y se usa para deformar el bloque. Sin embargo, el momento debe seguir conservándose. En consecuencia, el bloque se columpia con cierta rapidez. Después del choque, el bloque se comporta como un péndulo en el cual se conserva la energía mecánica total. Por esto, podemos usar la altura máxima del péndulo para determinar la energía cinética del bloque después del choque y luego, al usar la conservación del momento, podemos encontrar la velocidad inicial del proyectil.
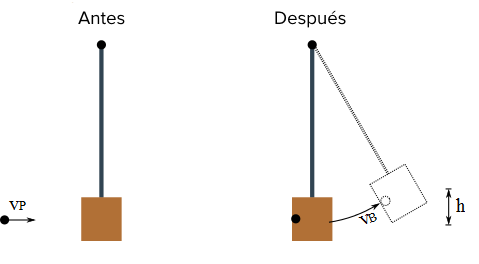
Figura 1: un choque inelástico en un péndulo balístico.
Figura 1: un choque inelástico en un péndulo balístico.
Sabemos que en este choque solo se conserva el momento. Así que el momento del proyectil antes del choque debe ser igual al momento del sistema proyectil-bloque inmediatamente después del choque. Aquí usamos el subíndice BBB para el bloque y PPP para el proyectil. v_BvBv, start subscript, B, end subscript es la velocidad del bloque justo después del impacto.
m_P v_{P} = (m_B + m_P) v_{B}mPvP=(mB+mP)vBm, start subscript, P, end subscript, v, start subscript, P, end subscript, equals, left parenthesis, m, start subscript, B, end subscript, plus, m, start subscript, P, end subscript, right parenthesis, v, start subscript, B, end subscript
Después de reacomodar:
v_{B} = \frac{m_P v_{P}}{m_P + m_B}vB=mP+mBmv, start subscript, B, end subscript, equals, start fraction, m, start subscript, P, end subscript, v, start subscript, P, end subscript, divided by, m, start subscript, P, end subscript, plus, m, start subscript, B, end subscript, end fraction
Sabemos que después del choque se conserva la energía mecánica del sistema bloque-proyectil, así que el bloque se eleva a una altura máxima hhh bajo la influencia de la aceleración gravitacional ggg, entonces:
\frac{1}{2} (m_P + m_B) v_B^2 = (m_P + m_B) gh21(mP+mB)vB2=(mP+mB)ghstart fraction, 1, divided by, 2, end fraction, left parenthesis, m, start subscript, P, end subscript, plus, m, start subscript, B, end subscript, right parenthesis, v, start subscript, B, end subscript, squared, equals, left parenthesis, m, start subscript, P, end subscript, plus, m, start subscript, B, end subscript, right parenthesis, g, h
Después de reacomodar:
v_B^2 = 2ghvB2=2ghv, start subscript, B, end subscript, squared, equals, 2, g, h
Al sustituir la velocidad inicial del bloque en nuestra expresión anterior de la conservación del momento:
\frac{m_P v_P}{m_P + m_B} = \sqrt{2gh}mP+mBm=2ghstart fraction, m, start subscript, P, end subscript, v, start subscript, P, end subscript, divided by, m, start subscript, P, end subscript, plus, m, start subscript, B, end subscript, end fraction, equals, square root of, 2, g, h, end square root
Así que después de un último reacomodo:
\boxed{v_{P} = \frac{m_P + m_B}{m_P} \sqrt{2gh}}vP=mPm2ghstart box, v, start subscript, P, end subscript, equals, start fraction, m, start subscript, P, end subscript, plus, m, start subscript, B, end subscript, divided by, m, start subscript, P, end subscript, end fraction, square root of, 2, g, h, end square root, end box
Ejercicio 2a: supón que se le dispara una munición a un bloque de 1 kg que es parte de un péndulo balístico. El bloque se columpia a una altura de 0,3 m. ¿Cuál es la rapidez inicial de la munición?
[Solución]
\begin{aligned} v_{P} &= \frac{0{,}01 + 1~\mathrm{kg}}{0{,}01~\mathrm{kg}} \sqrt{2\cdot 9{,}81~\mathrm{m/s^2} \cdot 0{,}3~\mathrm{m}} \\ &= 245~\mathrm{m/s} \end{aligned}Ejercicio 2b: supón que la munición del ejercicio anterior fuera reemplazada con una bala con la mitad de la masa y el doble de la rapidez inicial. ¿Sería seguro hacer el mismo experimento con el mismo aparato? ¿Esperarías el mismo resultado?
[Solución]
