Potencia Mecánica y Ejercicios de Cinemática

Potencia Mecánica

La potencia mecánica es una medida de la cantidad de energía suministrada a un paciente por un ventilador mecánico. Si bien la ventilación mecánica puede salvar vidas, también puede causar daño pulmonar, conocido como lesión pulmonar asociada con el ventilador. El ventilador induce tensiones en el pulmón del paciente, incluyendo barotrauma (presión), volutrauma (distensión), reotrauma (flujo rápido de gases) y atelectotrauma (colapso y reapertura repetida). La potencia mecánica mide estas tensiones para predecir la intensidad de la lesión pulmonar.

Ejercicios

Fórmulas

Enunciado del Ejercicio 3

Un observador a 40 m de altura ve un cuerpo subir con cierta velocidad y, tras 10 s, lo ve bajar a la misma velocidad.

a) ¿Cuál fue la velocidad inicial del móvil?

b) ¿Cuál fue la altura máxima alcanzada?

Usar g = 10 m/s²

Desarrollo

Datos:

t = 10 s

y = 40 m

Fórmulas:

(1) v_f = v₀ + g⋅t

(2) y = y₀ + v₀⋅t + ½⋅g⋅t²

(3) v_f² - v₀² = 2⋅g⋅h

Esquema:

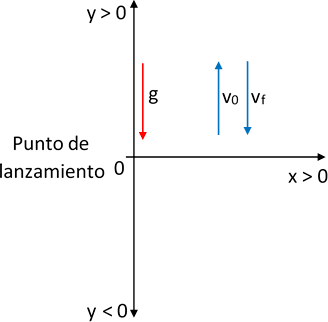
Sentido de los vectores en el tiro vertical hacia arriba

Solución

a)

Los 10 s se dividen en 5 s de subida (v_f = 0) y 5 s de bajada. Usando la ecuación (1):

0 = v₀ + g⋅t

v₀ = -g⋅t

v₀ = -(-10 m/s²)⋅(5 s)

v₀ = 50 m/s (a nivel del observador).

Esta velocidad inicial la usaremos como final en la ecuación (3):

v_f² - v₀² = 2⋅g⋅h

(50 m/s)² - v₀² = 2⋅(-10 m/s²)⋅(40 m)

(50 m/s)² - 2⋅(-10 m/s²)⋅(40 m) = v₀²

Resultado: v₀ = 57.45 m/s (a nivel de lanzamiento)

b)

Con la ecuación (3), calculamos la distancia desde el observador hasta la altura máxima:

v_f² - v₀² = 2⋅g⋅h

(0 m/s)² - (50 m/s)² = 2⋅(-10 m/s²)⋅h

h = 125 m

Sumamos la altura máxima y la altura del observador:

h = 125 m + 40 m

Resultado: h = 165 m

Enunciado del Ejercicio 5

Un auto choca a 60 km/h contra una pared. ¿Desde qué altura habría que dejarlo caer para el mismo efecto?

Usar g = 10 m/s²

Desarrollo

Datos:

v_f = 60 km/h = 16.67 m/s

v₀ = 0 m/s

Fórmulas:

(1) v_f = v₀ + g⋅t

(2) y = v₀⋅t + ½⋅g⋅t²

(3) v_f² - v₀² = 2⋅g⋅h

Solución

De la ecuación (3) con v₀ = 0:

v_f² = 2⋅g⋅h

Despejando "h":

h = v_f²/2⋅g

Reemplazando:

h = (16.67 m/s)² / [2⋅(-10 m/s²)]

Resultado: h = 13.9 m

Enunciado del Ejercicio 6

Se lanza una pelota hacia arriba y se recoge a los 2 s. Calcular:

a) ¿Con qué velocidad fue lanzada?

b) ¿Qué altura alcanzó?

Usar g = 10 m/s²

Desarrollo

Datos:

t = 2 s

Fórmulas:

(1) v_f = v₀ + g⋅t

(2) y = v₀⋅t + ½⋅g⋅t²

(3) v_f² - v₀² = 2⋅g⋅h

Esquema:

Sentido de los vectores en el tiro vertical hacia arriba

Solución

a)

Los 2 s se componen de 1 s de subida (v_f = 0) y 1 s de bajada. Con la ecuación (1):

0 = v₀ + g⋅t

v₀ = -g⋅t

v₀ = -(-10 m/s²)⋅(1 s)

Resultado: v₀ = 10 m/s

b)

Con la ecuación (2):

y = (10 m/s)⋅(1 s) + ½⋅(-10 m/s²)⋅(1 s)²

Resultado: y = 5 m