Propiedades Fundamentales del Álgebra y Resolución de Ecuaciones
Clasificado en Matemáticas
Escrito el en 
español con un tamaño de 10,24 KB
Leyes Fundamentales del Álgebra
Ley Conmutativa de la Adición y la Multiplicación
La primera ley fundamental del álgebra es la ley conmutativa de la suma y la multiplicación. Esta ley indica que la suma o el producto de dos números es el mismo, independientemente del orden en que se dispongan esos dos números. La notación de la ley conmutativa se representa como sigue:
- x + y = y + x
- xy = yx
Sustituyendo las variables por números se demuestra la veracidad de esta ley. Por ejemplo:
- 2 + 6 = 6 + 2 = 8
- 3 x 5 = 5 x 3 = 15
Para ilustrar mejor esta ley, observa que no funciona con la resta o la división.
Ley Asociativa de la Suma y la Multiplicación
La segunda ley fundamental del álgebra es la ley asociativa de la suma y la multiplicación. Esta ley establece que la suma o producto de tres o más números es el mismo, independientemente de cómo se agrupen. Por lo tanto:
- x + (y + z) = (x + y) + z
- x(yz) = (xy)z
Nuevamente, al sustituir las variables por números, podemos comprobar que la ley es verdadera:
- 2 + (3 + 5) = (2 + 3) + 5 = 10
- 2 x (3 x 5) = (2 x 3) x 5 = 30
Ley Distributiva
La tercera ley fundamental del álgebra es la ley distributiva. Esta ley establece que el producto de un número por la suma de otros dos es igual a la suma de los productos de ese número por cada uno de los sumandos. La notación de la ley distributiva es la siguiente:
- x(y + z) = xy + xz
Sustituyendo las variables por números se demuestra una vez más la aplicación de esta ley:
- 3(4 + 6) = (3 x 4) + (3 x 6) = 12 + 18 = 30
Importancia de las Leyes Básicas del Álgebra
Es fundamental comprender que las leyes básicas del álgebra son la piedra angular para entender su aplicación. Muchos estudiantes cometen el error de aprender a resolver problemas algebraicos mecánicamente, sin reflexionar sobre cómo se derivan las reglas y leyes algebraicas. Los estudiantes que dedican tiempo a estudiar el origen de estas leyes, reglas y teoremas desarrollan una mejor comprensión de las aplicaciones prácticas del álgebra.
Reglas para Resolver Ecuaciones de Primer Grado
Regla de la Suma (Transposición de Términos)
Regla de la suma: Si a los dos miembros de una ecuación sumamos la misma expresión algebraica, obtenemos una ecuación equivalente.
Ejemplo:
Podemos sumar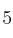 
a ambos miembros:
Así obtenemos:
En la práctica, esta regla se conoce como transposición de términos: un término que está sumando en un miembro pasa restando al otro miembro, y viceversa (un término que está restando pasa sumando).
Ejemplo:
Los términos 
y 
podemos pasarlos al segundo miembro (cambiándoles el signo):
Así la ecuación quedaría:
Regla del Producto (Despejar la Incógnita)
Regla del producto: Si multiplicamos o dividimos ambos miembros de una ecuación por un mismo número (distinto de cero), resulta otra ecuación equivalente.
Ejemplo:
Si dividimos ambos miembros por 
, obtenemos:
Así obtenemos:
En la práctica: un factor que está multiplicando en un miembro pasa al otro miembro dividiendo, y un divisor pasa multiplicando. El objetivo es despejar la incógnita.
Ejemplo:
Queremos despejar la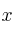 
(dejarla sola).
Para ello, el 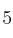que está multiplicando, lo pasamos al otro miembro dividiendo:
Resolución de Sistemas de Ecuaciones Lineales
Método de Sustitución
Pasos del Método de Sustitución
- Despejar: Despeja una incógnita en una de las dos ecuaciones. Es recomendable elegir la incógnita con el coeficiente más sencillo (1 o -1).
- Sustituir: Sustituye la expresión obtenida para esta incógnita en la otra ecuación. Resultará una ecuación con una sola incógnita.
- Resolver: Resuelve la ecuación de una incógnita obtenida en el paso anterior.
- Hallar la otra incógnita: Sustituye el valor encontrado en la expresión donde despejaste la primera incógnita (del paso 1).
- Solución: Los dos valores hallados (uno para cada incógnita) forman la solución del sistema de ecuaciones.
Ejemplo de Aplicación del Método de Sustitución
Consideremos el sistema:
1. Despejamos una de las incógnitas en una de las dos ecuaciones. Elegimos la incógnita x de la primera ecuación, ya que tiene el coeficiente más bajo (implícitamente 1).
2. Sustituimos en la otra ecuación (la segunda) la variable x, por la expresión obtenida:
3. Resolvemos la ecuación de una incógnita (y) obtenida:
4. Sustituimos el valor obtenido (y = 2) en la expresión donde despejamos x (del paso 1).
5. Solución del sistema:
