Ingles lengua

Escrito el 15 de Agosto de 2012 en español con un tamaño de 11,39 KB

Propiedades generales

Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguiente propiedades:

Límite de	Expresión
Una constante	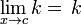$\lim_{x \to c} k =\, k\,$
La función identidad	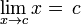$\lim_{x \to c} x = \, c \,$
El producto de una función y una constante	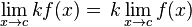$\lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,$
Una suma	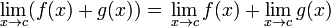$\lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,$
Una resta	$\lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,$
Un producto	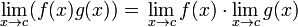$\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,$
Un cociente	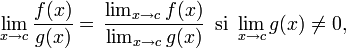$\lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,$
Una potencia	${\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0$
Un logaritmo	${\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}$
El número e	${\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e$
Función f(x) acotada y g(x) infinitesimal	${\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0$ .

LIMITE EXISTE PARA CUANDO X TIENDE A X0.
EXISTE EL TEOREMa DEL LIMITE QUE DICE QUE PARA QUE EXISTA DEBE CUMPLIR CON 3 CONDICIONES:
PRIMERO QUE F(X) ESTE DEFINIDA,ES DECIR QUE LA FUNCION QUE ESTAS ANALIZANDO EXISTA Y SEA CONTINUA, PUES SI HAY DISCONTINUIDAD EL LIMITE NO EXISTIRA.
SEGUNDO QUE LOS LIMITES LATERALES SEAN IGUALES, ES DECIR QUE LLEGUES AL MISMO VALOR POR LA IZQUIERDA Y DERECHA.
TERCERO, QUE F(X0)= LIM F(X), ES DECIR, QUE SI LA FUNCION VALUADA EN ESE PUNTO ES IGUAL AL LIMITE EN ESE PUNTO, EL LIMITE EXISTIRA, SE DEBERAN CUMPLIR ESTAS 3 CONDICIONES PARA SU EXISTENCIA, PUES SI NO SE CUMPLE AUNQUE SEA UNA SE PUEDE DECIR QUE NO EXISTE. TAL VEZ CON UN EJEMPLO TE QUEDARIA MAS CLARO

Propiedades generales

Entradas relacionadas: